Als ersten Schritt einer Kurvendiskussion untersucht man die Bereiche, für die eine Funktion gültig ist.
Zunächst einmal zum Verständnis, was diese beiden Dinge bedeuten.
Sehr, sehr, streng mathematisch ist eine Funktion, die einen Definitionsbereich und einen Zielbereich hat. Die Funktion ordnet jedem Element des Definitionsbereichs genau ein Element des Zielbereichs zu.
Im einfachsten Fall, f(x)=x sind Definitions- und Zielbereich beide schlicht alle reellen Zahlen. In anderen Fällen ist dies komplizierter. Betrachten wir dazu:
Bedenken wir, was mit der Funktion passiert. Im Nenner setzen wir unser x ein, ziehen davon zwei ab und quadrieren es dann. Dadurch, dass es quadriert wird, ist es immer positiv. Hey, das schränkt den Zielbereich ein – auf alle positiven Werte!
Natürlich gibt es ein Problem – denn wenn wir x = 2 betrachten, erhalten wir f(2) = 1/0² = 1/0 – wir teilen durch 0. Natürlich wissen wir längst, dass teilen durch 0 nicht möglich ist. Also erhalten wir für x = 2 auch keine richtige Zahl. Aber damit es eine Funktion ist, muss es jeder Zahl seines Definitionsbereichs eine Zahl zuordnen.
Das ganze ist nur halb so problematisch wie es scheint – wir müssen nicht verzweifelt versuchen, einen vernünftigen Wert für x=2 zu finden, sondern gehen es pragmatisch an – und bannen 2 aus dem Definitionsbereich. Aber alle anderen Reellen Zahlen lassen wir zu.
So ergibt sich also:
Die erste Zeile bedeutet „Alle Reellen Zahlen außer 2“, die zweite „Alle Reellen Zahlen größer als 0“. Dies ist die Mengenschreibweise.
Ebenso gebräuchlich ist die Intervallschreibweise. In dieser würde es
Definitionsbereich: [-∞, 2) ∨ (2, ∞]
Zielbereich: (0, ∞]
heißen.
Es gibt kein striktes Verfahren zum finden der Definitions- und Zielbereiche. Hier kommt uns nur der begrenzte Umfang der Schulaufgaben zugute.
Definitionsbereiche sind für gewöhnlich nur auf zwei Weisen eingeschränkt:
- Durch Definitionslücken
Definitionslücken sind einzelne Punkte einer Funktion die nicht definiert sind, während jeder angrenzende Wert es ist. Diese entstehen nahezu nur durch Teilung. Achtet man also auf Brüche in der Funktion, kann man prüfen, ob der Nenner Nullstellen hat. Wenn ja, sind diese auch Definitionslücken. - Durch begrenzt definierte Funktionen.
Dies sind elementare Funktionen, die nicht überall definiert sind. Die wichtigsten Vertreter:- √x – Als Umkehrfunktion von x², welches alle Werte positiv macht, kann √x selbst keine negativen Werte verarbeiten. 0 ist allerdings gültig.
- log (x) – log(x) ist die Umkehrfunktion der Exponentialfunktion – die, ebenso wie die Quadratfunktion, alles positiv macht. So kann auch die Logarithmusfunktion keine Werte die größer als 0 sind verarbeiten – auch 0 selbst ist hier ausgeschlossen.
- tan(x) – Der tangens ist definiert als sin(x)/cos(x) und cos(x) hat bei 90°, 270° (und nach jeweils weiteren 180°) Nullstellen. Dadurch hat auch der Tangens seine Definitionslücken bei den selben Werten.
Zielbereiche lassen sich meist durch etwas Überlegung herausfinden. Häufig ist es ratsam, zunächst ein wenig Platz freizulassen und das Verhalten in der Unendlichkeit zu untersuchen. Geht die Funktion nämlich sowohl gegen + unendlich wie auch – unendlich ergibt sich sofort, dass der Zielbereich jede Reelle Zahl einschließt. Ist dies nicht der Fall, muss man auch noch die Extremstellen zu Rate ziehen.
Man schreibt sich in diesem Fall die Y-Werte aller Hoch- und Tiefpunkte sowie die Werte, die sich in der Unendlichkeit ergeben heraus.
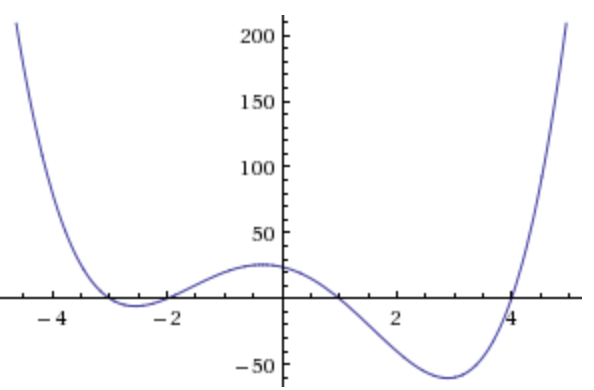
Hier zum Beispiel wären dies:
Unendlich, -10, 30, -60, Unendlich.
Nun nehmen wir das größte und kleinste aus dieser Liste und erhalten den Definitionsbereich:
[-60, Unendlich]
Wenn dies geschafft ist geht es weiter zu Schritt 2: Nullstellenbestimmung.