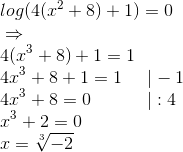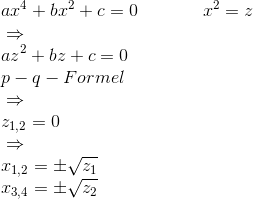Nullstellenbestimmung ist der zweite Schritt einer Kurvendiskussion. Im Schritt davor untersucht man Definitions- und Zielbereich.
Das Bestimmen von Nullstellen ist weitestgehend durch das Auflösen einer Gleichung nach 0 zu erledigen. Das rein arithmetische Umformen wird hier allerdings nicht behandelt. Stattdessen gibt es einige Kniffe, die an dieser Stelle in Erinnerung gerufen werden sollten. Darüber hinaus gibt es einige elementare Funktionen, deren Nullstellen bekannt sein müssen, um alle Gleichungen lösen zu können.
Nullstellen elementarer Funktionen:
In der letzten Zeile ist eine sehr wichtige Beobachtung, die keine Nullstelle ist: Der Umstand, dass ex niemals 0 ist.
Nullstellen verketter Funktionen
Die obigen Nullstellen sind besonders in verketten Funktionen wichtig. Denn wenn wir diese kennen, können wir unsere Berechnungen oft einfacher machen.
Sicherlich kein schönes Ergebnis – aber es war leicht zu errechnen, nachdem man den Logarithmus entkommen ist. (Zu beachten: Wir ziehe die dritte Wurzel, also ist es in Ordnung, dass wir eine negative zahl unter der Wurzel haben).
Deswegen ist es absolut wichtig, die wenigen obigen Nullstellen zu kennen.
Nullstellen multiplizierter Funktionen
Wir rufen uns nur für einen Moment in Erinnerung, dass 0*x = 0 ist – vollkommen und absolut unabhängig von x. Dann wird uns schnell klar, wie multiplizierte Funktionen einfach zu durchsuchen sind: Indem man die Nullstellen der Faktoren einzeln sucht.
Hier haben wir x³ ausgeklammert (ebenfalls ein sehr wichtiges Werkzeug) und dann die drei Faktoren herausgeschrieben. Aus diesen sind die Nullstellen nahezu sofort sichtbar.
ex hat keine Nullstelle.
x³ hat seine Nullstelle bei x=0
Bei x² – 4 rechnen wir + 4 und ziehen die Wurzel, wodurch wir ±2 erhalten.
p-q-Formel:
Altbekannt doch leicht vergessen: Die p-q-Formel. Zu beachten ist:
- Die Funktion muss normalisiert sein (x² muss den koeffizienten 1 haben, wenn man stattdessen ax² hat, einfach durch a teilen).
- p und q dürfen auch 0 sein.
- Am einfachsten ist es, -p/2 vor der klammer auszurechnen und dies dann direkt (im Zweifelsfall per Taschenrechner) zu quadrieren und in die Wurzel zu schreiben.
- Ergibt sich ein negativer Wert unter der Wurzel heißt das nicht, dass ein Fehler begangen wurde – es kann auch einfach keine Nullstelle geben.
Substitutionsverfahren:
Dieses Verfahren funktioniert nur dann, wenn ausschließlich x4 und x² vorhanden sind. (Technisch gesehen mit jedem Paar Exponenten, die gerade sind und in einem Verhätlnis von 1/2 zueinander stehen, diese treten jedoch im schulischen Rahmen nicht auf).
Es ist simpel: Man ersetzt x² durch z, indem man behaupt, z wäre das gleiche. Jetzt hat man eine Form, in der die p-q-Formel anwendbar ist. So erhält man bis zu 2 Ergebnisse. Resubstituiert man dann am Ende, werden daraus bis zu 4 Nullstellen. Genaueres in den Beispielen.
Die Kurvendiskussion geht mit Symmetriebetrachtungen weiter.