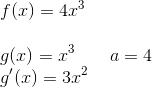Die Faktorregel ist eine kleine Ableitungsregel und ein Sonderfall der Produktregel.
Formale Definition:
Es gilt also: Konstanten, die mit einer variablen Funktion multipliziert werden, verändern sich beim Ableiten nicht.
Anzuwenden bei:
Das bedeutet: Die Faktorregel wird verwendet, wenn eine konstante Zahl mit einer regulären Funktion multipliziert wird.
Hier stellt das dritte Beispiel eine Funktionenschar dar. Auch wenn a nicht exakt bestimmt ist, ist es eine konstante Zahl.
Anwendungsverfahren:
Wir betrachten unser erstes Beispiel. Während diese Regel in der Praxis nahezu immer im Kopf angewandt wird, wird sie hier dennoch sehr kleinschrittig bearbeitet.
Wir ermitteln also a und g(x), leiten g(x) ab und setzen beides in die Formel ein.
Nachdem wir alles ausmultipliziert und die Funktion damit so weit wie möglich vereinfacht haben ist die Ableitung fertig.
Beweis:
Die Faktoregel folgt direkt aus der Produktregel. Wenn wir die Produktregel anwenden, ergibt sich folgendes:
Im ersten Schritt haben wir die Produktregel nur formelmäßig angewandt. Erst im zweiten Schritt schreiben wir die Ableitung von a, vorher als a‘ bezeichnet, auf: 0. Die Ableitung einer konstanten Zahl ist immer 0.
Dadurch fällt die linke Seite der Summe weg, die rechte bleibt und gibt uns unsere obige formale Definition.