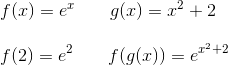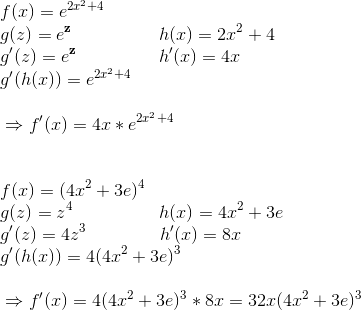Die Kettenregel ist, gemeinsam mit der Produktregel, eine der zwei wichtigen Ableitungsregeln für komplexe Ableitungen.
Formal wird sie benutzt, wenn eine Funktion in eine andere „eingesetzt“ – verkettet – wird. Die formale Definition einer Verkettung ist nicht ganz einfach, aber glücklicherweise sind verkettete Funktionen meist leicht genug zu erkennen. Hier ist zunächst ein Beispiel, wie eine Verkettung zustande kommt.
Zunächst habe ich mir zwei beliebige Funktionen f und g genommen. Die linke Seite, beim Einsetzen der 2, ist dort, um noch einmal mit einem einfachem und bekanntem Fall zu zeigen, was passiert, wenn man etwas in eine Funktion einsetzt – alle Variablen dieser Funktion werden durch den eingesetzten Wert ersetzt.
Ebenso ist es rechts – wir setzen eine ganze Funktion ein, also wird jedes x durch diese Funktion ersetzt.
Mit diesem Vorwissen gehen wir zur Definition.
Formale Definition:
Das bedeutet: Wir nehmen die Ableitung der „inneren“ Funktion h und multiplizieren sie mit der Ableitung der „äußeren“ Funktion g, in das noch immer h eingesetzt ist. Hierbei wird von Lehreren immer wieder gern der Merksatz „innere Ableitung mal äußere Ableitung“ oder, kürzer, „innere mal äußere“ an die Köpfe der Schüler geworfen. Das macht die Kettenregel in der Definition recht leicht zu merken, ist aber deshalb noch nicht leicht in der Anwendung.
Anzuwenden bei:
Diese Funktionen sehen auf den erstem Blick erschrecked aus, aber sie lassen sich gut systematisch lösen.
Anwendungssystem:
Der erste Schritt ist immer, herauszufinden welches die innere und äußere Funktion sind. Meist ist dies glücklicherweise nicht sehr schwer.
Dann schreiben wir die innere und äußere Funktion heraus und leiten sie ab. Wichtig ist, dass wir aus formalen Gründen die äußere Funktion nicht als g(h(x)), sondern als g(z) abschreiben. Dies dient dazu, die Ableitung von g einfacher zu gestalten – h(x) wird später wieder eingesetzt, oder auch resubstituiert.
Nachdem wir innere und äußere Funktion abgeleitet haben, setzen wir die Ergebnisse in die Formel ein. Die folgenden zwei Beispiele sollten dem Verständnis helfen.
Hält man sich eng an dieses Verfahren kann kaum etwas schiefgehen. Auch die Kettenregel kann mit etwas übung komplett im Kopf gelöst werden, aber das schriftliche Aufteilen kann stets Unsicherheiten beseitigen.
Nun ist noch zu lernen, die Ketten- und Prouktregel zu verknüpfen. Dann lassen sich entgültig alle Funktionen (die im schulischen Rahmen auftreten) lösen.