Wenn die Ableitungsregeln alle bekannt sind lässt sich viel erreichen, jedoch müssen diese manchmal gemeinsam miteiandner verwendet werden. Systematisch ist dies nicht übermäßig kompliziert. Hier zeige ich drei komplexere Beispiele, die dem Verständnis vielleicht weiterhelfen. Am wichtigsten ist hierbei jedoch immer, den Überblick zu behalten. Wenn derartige Funktionen auftreten und man sie ableiten soll, ist es das beste, sich viel Platz auf dem Papier zu nehmen um strukturiert vorgehen zu können.
Diese drei Unterscheiden sich in der Vorgehensweise.
In der ersten Funktion müssen wir zunächst die Produktregel anwenden, und wollen für diese die Ableitung des rechten e-Faktors herausfinden, wofür wir die Kettenregel benötigen.
In der zweiten Funktion wenden wir erst die Kettenregel an, benutzen dann jedoch die Produktregel für die innere Ableitung.
In der dritten Funktion benötigen wir erst die Quotienten-, dann die Produktregel.
In jeder der drei Aufgaben geht es sehr strikt vor: Wir wenden blind die Regeln an und schreiben die Bestandteile heraus. Wenn an dieser Stelle alle Ableitungen sofort ersichtlich sind, fertigen wir sie an und setzen sie in die Ableitung ein. Wenn nicht, betrachten wir die Teilfunktion die uns Probleme bereitet und wenden an dieser Stelle wieder eine passende Regel an, so lange, bis wir alle Bestandteile haben, um sie dann schließlich einzusetzen. Dieses Schema gelingt (für Funktionen, die im schulischen Rahmen auftreten) immer.
Erste Funktion:
Am Ende haben wir zwei verschiedene Darstellungen von f ‚, von denen keine strikt besser ist. Die erste ist leichter ein zweites mal abzuleiten, mi der zweiten finden sich Nullstellen leichter.
Zweite Funktion:
Auch hier haben wir wieder ein kompliziertes Endergebnis, welches wir je nach Anwendung umformen können.
Dritte Funktion:
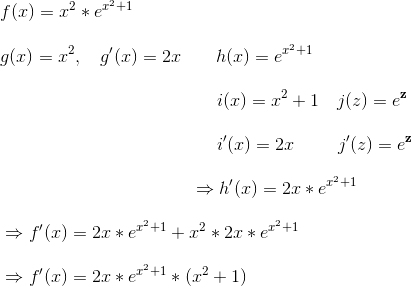
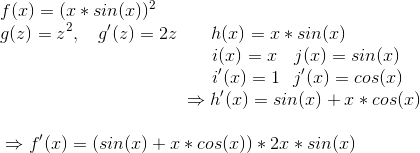
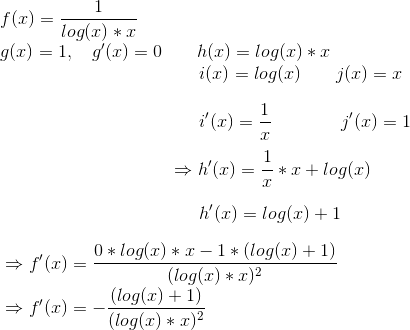
in der dritten Funktion zum abletien sollte es ln(x) sein und nicht log(x), weil 1/x die Ableitung von ln(x) ist und nicht von log(x)