Der dritte Schritt der Kurvendiskussion: Symmetriebetrachtung Im Schritt davor betrachteten wir Nullstellen.
Grundgedanke:
Wenn die Symmetrie einer Funktion gezeigt ist, lässt sich viel Arbeit ersparen – Alles wird gespiegelt, so auch Nullstellen, Extremstellen, Wendestellen und Verhalten in der Unendlichkeit.
Es gibt zwei Formen vom Symmetrie die wir untersuchen: Achsensymmetrie und Punktsymmetrie.
Achsensymmetrie lässt sich gut am Beispiel x² erkennen, Punktsymmetrie am Beispiel x³.
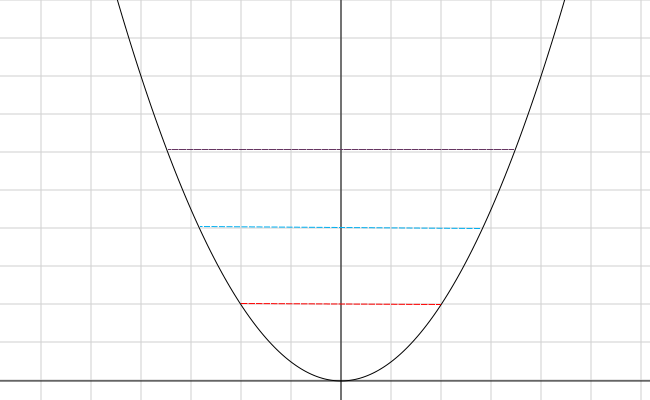
Betrachten wir die folgenden Graphen:
Definition:
x² ist gespiegelt entlang der y-Achse – graphisch bedeutet das, dass man von jedem Punkt der Funktion in kürzester Strecke zur Y-Achse gehen kann, diese Strecke dann verdoppelt und wieder an einem Punkt des Graphen landet.
In einer Formel ausgedrückt lässt sich Achsensymmetrie sehr einfach definieren und testen:
Achsensymmetrie ist gegeben, wenn:
![]()
gilt.
x³ ist gespiegelt am Punkt (0, 0), dem Ursprung. Graphisch gesehen heißt dass, dass man von jedem Punkt der Funktion einen Strich zu (0, 0) ziehen kann und man wieder auf einem anderen Punkt der Funktion landet, wenn man diese Strecke verdoppelt.
Indem man es sich als eine Spiegelung der y- und x-Achse vorstellt, kann man dies genauso einfach Mathematisch definieren und prüfen.
Punktsymmetrie ist gegeben, wenn
gilt.
Beispiele
Hier ein paar Rechenbeispiele, an denen der Umgang mit den Formeln erkenntlich werden sollte.
Im ersten Schritt haben wir nur angekündigt, dass wir Gleichheit prüfen werden.
Im zweiten Schritt haben wir die Funktion eingesetzt. Rechts haben wir dabei jedes x durch -x ersetzt. Wichtig ist dann, dass das -x in Klammern steht!
Im dritten Schritt haben wir für die geraden Exponenten überlegt, dass es keinen Unterschied macht, ob x oder -x eingesetzt wird. Daher können wir mit Gewissheit das Minuszeichen entfernen.
Nun sind beide Seiten gleich und Achsensymmetrie folgt.
Weitere Beispiele:
Im ersten Beispiel nutzen wir die Tatsache, dass (-x)³ = -x³ ist. Nachdem wir festgestellt haben, dass es keine Achsensymmetrie gibt, beginnen wir den Vorgang nicht von vorn, sondern drehen alle Vorzeichen um – dadurch prüfen wir ohne weiten Aufwand sofort auf Punktsymmetrie.
Das gleiche geschieht auch im zweiten Beispiel. Hier tritt allerdings keine der Symmetrien auf.
Zusammenfassend:
Wir beobachten:
Wenn wir f(-x) betrachten, so bleibt das Vorzeichen bei geraden Exponenten gleich, bei ungeraden dreht es sich.
Wenn wir -f(-x) betrachten, so dreht sich das Vorzeichen bei geraden Exponenten, bei ungeraden bleibt es gleich.
Daraus generalisieren wir:
Eine Polynomfunktion ist genau dann Achsensymmetrisch wenn, sie nur positive Exponenten (dazu zählt auch eine Konstante am Ende, wie etwa +3) besitzt.
Eine Polynomfunktion ist genau dann Puntsymmetrisch wenn, sie nur negative Exponenten (ohne Konstaten) besitzt.
Mit diesen Regeln kommt man schon sehr weit. Nur selten wird die Symmetrie bei nicht-polynomen Funktionen beobachtet, aber im Zweifelsfall können immer die obigen Formeln verwendet werden. Oft lässt sich das Problem auch optisch lösen: ex ist nicht Symmetrisch – Dies sollte jeder Lehrer mit Verweis auf den Wohlbekannten Verlauf des Graphen bereits als Antwort akzeptieren. (Auch hier gilt natürlich: Immer individuelle Regeln mit der Lehrerkraft besprechen um festzustellen welche Grenzen der „intuitiven Logik“ gesetzt sind).
Im nächsten Schritt der Kurvendiskussion betrachten wir das Verhalten im Unendlichen.

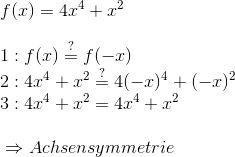
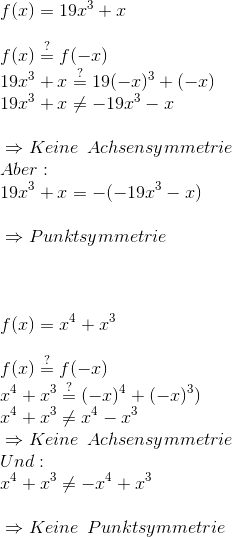
Soweit ich weiß:
Wenn du etwas untersucht, dann setzt du in die Funktion ein.
Bei der Symmetrie wäre es falsch zu sagen, dass die Funktion punktsymmetrisch zum Ursprung ist, wenn f(x)=-f(-x) gilt.
Der allgemeine Ansatz zum Berechnen der Symmetrie lautet:
Achsensymmetrie zur y-Achse: f(-x)= f(x).
Punktsymmetrie zum Ursprung: f(-x)=-f(x).
Wenn du f(x) da stehen hast, dann rechnest du nichts aus.
Hast du aber f(-x) da stehen, dann sagst das aus, dass du auf die Symmetrie untersuchst. Je nachdem, wie das Ergebnis ausfällt, hast du dann deine Symmetrie.
Um zu wissen, ob du recht hast, kannst du dir auch die Exponentenregel bedienen.
Sie besagt:
Nur gerade Exponenten –> achsensymmetrie
nur ungerade Exponenten –> punktsymmetrisch
beides –> weder punkt- noch achsensymmetrisch.
Das was das Auge sieht, dient nur der Überprüfung !!!
Das Berechnete ist ausschlaggebend!!
Hoffe konnte dir helfen