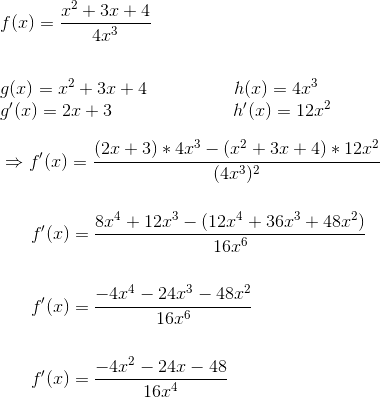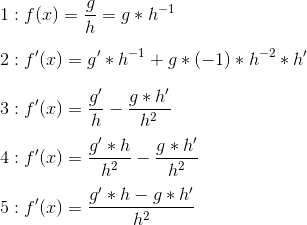Die Quotientenregel ist ein Sonderfall der Produktregel und vereinfacht das Ableiten von Funktionen die sich teilen, beziehungsweise negative Exponenten haben.
Formale Definition:
Die Ähnlichkeit zur Produkregel ist nicht sofort offensichtlich. Man kann sich jedoch im Zähler klar machen, dass es dort aufgrund des negativen Exponenten von h ein minus statt eines plus gibt, wodurch die Ähnlichkeit größer wird. Eine vollständige Herleitung der Regel ist im Beweis unten.
Anzuwenden bei:
Die Funktionen, in denen diese Regel anwendbar ist, sind meist extrem offensichtlich. Ausnahmen stellen eventuell Funktionen dar, die einen negativen Exponenten anstatt eines Bruchstrichs verwenden (wie im dritten Beispiel). Mit etwas Übung in der Umformung von Exponenten wird dies aber auch schnell sichtbar. Und selbst wenn nicht, kann die Produktregel verwendet werden.
Anwendungssystem:
Wie üblich kann auch dieses System oft im Kopf gelöst werden. Um es zu systematisch zu lösen, müssen lediglich g, g‘, h und h‘ bestimmt werden.
Wir sehen also: Das Ableiten der Funktion ist nicht schwer, das Ergebnis ist jedoch oft sehr unschön und kann drastisch vereinfacht werden – was besonders bei wiederholten Ableitungen wichtig ist. Wichtig ist, dass auf Klammern geachtet wird – bestehen g, h, g‘ oder h‘ aus mehreren Summanden müssen Klammern gesetzt werden, wenn man nicht schon im ersten Schritt im Kopf alles ausmultiplizieren möchte, was sehr fehleranfällig wäre.
Beweis:
Betrachten wir die Ausgangslage mit der Produktregel:
1: Zunächst formen wir in die Potenzschreibweise um.
2: Nun haben wir die Produkregel angewandt. Wichtig ist hierbei, dass h-1 mit der Ketenregel bearbeitet wird. Die Innere Funktion ist h, die äußere ist z-1.
3: Wir formen in die Bruchschreibweise zurück
4: Die linke Seite wird um h/h erweitert.
5: Die Formel ist erfolgreich hergeleitet und damit bewiesen.