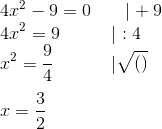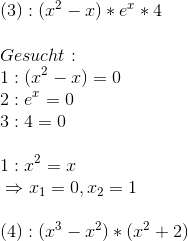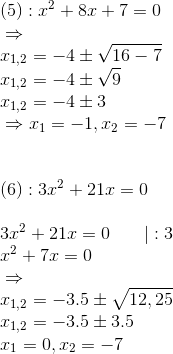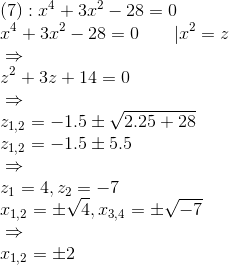Nullstellenbestimmung ist der zweite Schritt einer Kurvendiskussion. Hier finden sich Beispiele zu jedem der erklärten Verfahren.
Nullstellen eines Polynoms
Zum Beginn doch ein kleines Beispiel für die Arithmetische Umformung eines simplen Polynoms.
Solange man mit dem Auflösen von Gleichungen vertraut genug ist um zu wissen, wann addieren/substrahieren und wann multiplizieren/dividieren muss wird es hier nie Probleme geben.
Nullstellen verketter Funktionen
Ein Beispiel befand sich schon in den ursprünglichen Erklärungen. Hier ein weiteres
Als Bonus ist Aufgabe (2) zur Selbstübung gelassen. Die Lösung ist am Ende der Seite.
Nullstellen multiplizierter Funktionen
(4) zum Selbstlösen, Antworten am Ende der Seite.
p-q-Formel:
Hier gibt es nichts zu beachten.
Substitutionsverfahren:
x3, 4 existieren nicht, aber das ist kein Problem.
Lösung zu den Aufgaben:
(2): Es ist eine Exponentialfunktion, es gibt also keine Nullstellen.
(4): Die Lösungen sind ±√(2), 0 und 1.